설탕 배달(2839)
설탕 배달 문제(2839)를 세가지 방법으로 풀어봅니다.
문제 📄
입력으로 N kg의 설탕이 주어질 때, 상근이는 3, 5kg 봉지만으로만 N kg을 만들어서 배달한다. 이때 총 봉지의 최소 개수를 출력해야한다. 3,5kg으로 주어진 N을 만들 수 없다면 -1을 출력해야한다. (N은 3이상 5000이하의 정수이다.)
1. 상식적인 풀이 💡
상식적으로 무거운 5kg짜리를 더 많이 들고가면 상대적으로 3kg짜리는 덜 들고간다. 즉 5kg짜리가 많을수록 전체 봉지수는 적어진다.
- 주어진 입력 N에서 3을 계속해서 뺀다.
- 3을 뺀 횟수는 바로 3kg 짜리 봉지의 개수이다.
- 계속 빼다가 N이 5의 배수가 된다면 멈춘다. 이 값을 5로 나눈 몫이 5 kg짜리의 개수이다.
- 만약 음수가 되었다면 -1을 출력한다. 주어진 입력 N에서 3을 빼서 0이상의 5의 배수를 만들 수 없다. 즉 3, 5의 배수의 합으로 N을 만들 수 없음을 말한다.
코드 💾
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def main()->None:
N = int(input())
three_count = 0
# 음수가 아닌 동안 3씩 빼며 5의 배수로 만들기
while N >= 0:
if N % 5 == 0:
print(three_count + N // 5)
return
else:
N -= 3
three_count += 1
# N을 5의 배수로 만들 수 없음.
print(-1)
if __name__ == "__main__":
main()
2. 수학적 풀이 📊
3kg 봉지를 $x$개, 5kg 봉지를 $y$개 들고 간다고 할때, $N=3x+5y$이고 구해야하는 것은 $x+y$의 최솟값이다. 이때 $x,y$는 0이상의 정수이다.
\[\begin{equation} x+y = x + \frac{N-3x}{5}= \frac{N+2x}{5} \label{eq:label_one} \end{equation}\]$N=3x+5y$에서 $x$에 관해 정리하고, $x+y$의 $y$에 대입하면 $x+y$는 증가하는 일차함수이다.
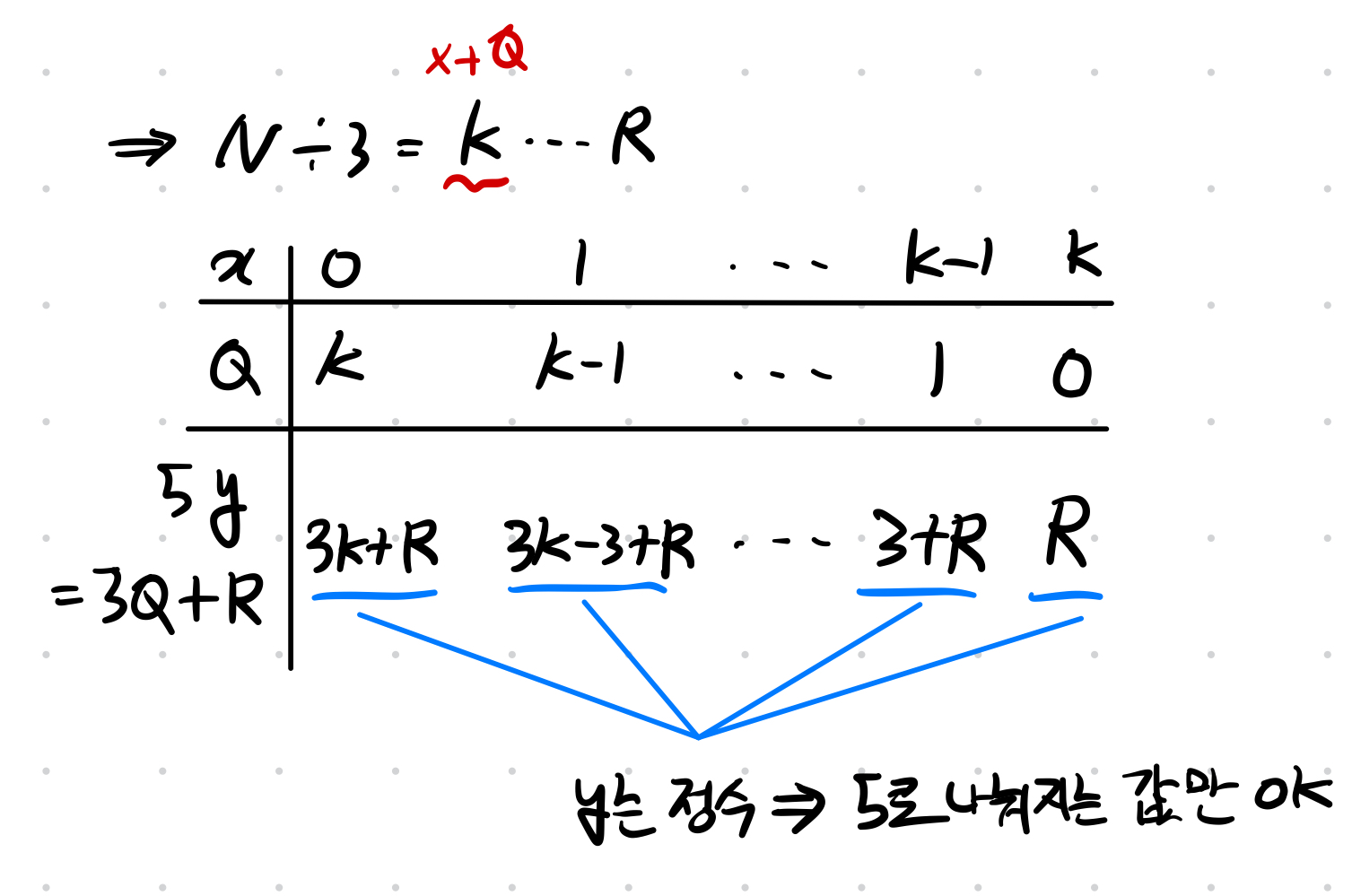
\[\begin{equation} 5y = 3Q + R \label{eq:y_def} \end{equation}\]그리고 $5y$를 $3Q(Q=0,1,2,\cdots)$와 나머지 $R(=0,1,2)$의 합으로 되어있다고 하자.
\[\begin{split} N &= 3x + 5y = 3x + (3Q + R) \\ &= 3(x+Q) + R \end{split}\]그러면 $N$을 3의 배수와 나머지 $R(=0, 1, 2)$의 꼴로 만들 수 있다.
$x+Q = k$라 두면 $N \div 3 = k \cdots R$이다. $x$는 0이상의 정수 이므로 위의 표처럼 $x, Q$ 값들을 나열해 볼 수 있다. 이때 \eqref{eq:y_def} (5y = 3Q + R)으로 했고, 세번째 행에는 $5y$의 값들을 나열했다.
이때 $y$도 0이상의 정수가 되어야하므로 $3Q+R$의 값이 5의 배수가 되어야 정수 $y$ 값을 구할 수 있다.
\eqref{eq:label_one}에 의해 $x+y$는 항상 증가하고, 제일 처음 만나는 5의 배수 $3Q+R$의 값에서 5를 나눠 $y$를 구해 가장 최소인 $x+y$의 값을 찾으면 된다.
그러고 만약에 5의 배수인 $3Q+R$을 끝까지 찾지 못했다면 정수 $y$값을 찾을 수 없으므로 -1을 출력하면 된다.
코드 💾
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def main() -> None:
N = int(input())
"""
N = 3x + 5y이고, 5y = 3Q+R (R = 0,1,2)라 하자.
N = 3x + 3Q + R
= 3(x + Q) + R
= 3 * quot + R
"""
quot, R = N // 3, N % 3
# x = 0부터 차례로 탐색
# 5의 배수인 3Q+R를 처음 구하면 답을 출력하고 종료
for x in range(0, quot + 1):
# x + Q = quot
Q = quot - x
five_y = 3 * Q + R
# 3Q + R이 5의 배수면 y 탐색 성공
if five_y % 5 == 0:
print(x + five_y // 5)
return
# 5의 배수인 3Q+R을 찾지 못함.
print(-1)
if __name__ == "__main__":
main()
반복문의 반복횟수는 $\frac{N}{3}$번 이기에 시간 복잡도는 (아마도) $O(N)$이다.
3. Dynamic Programming 풀이
주어진 입력 N kg을 생각해보면, N-3 kg을 3,5kg으로 어떻게든 만들고, 거기에 3kg 한봉지를 더하면 된다. 비슷하에 N-5 kg도 마찬가지이다.
\[\text{answer}[N] = \text{min}(\text{answer}[N-3], \text{answer}[N-5]) + 1\]그렇다면 우리가 알고싶은 N kg을 만드는 최소 봉지 개수는 위와 같이 둘 중에 작은 값에 한 봉지를 더하면 된다. 즉 주어진 N kg에 대한 문제를 두 개의 소문제(Subproblem)로 쪼개어 분석했다. 이런식으로 계속 쪼개다보면 쉽게 구할 수 있는 작은 숫자까지 내려가고, 거기서부터 계산을 해서 거꾸로 올라가면 N kg에 대한 답을 구할 수 있다.
(N은 3~5000사이의 값) 4kg은 3,5kg 봉지로 만들 수 없으므로 답은 -1이고, 3,5kg은 각각 3,5kg 한 봉지로 만들 수 있으므로 답은 1이다. 그리고 6부터 N까지 반복문을 통해 위의 min(...) + 1의 식을 써서 Bottom-up 방식으로 문제의 답을 구할 수 있다.
코드 💾
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def main() -> None:
N = int(input())
# 3 ~ 5000kg 까지 답을 저장할 배열
dp = [-1] * 5001
# 3, 5kg은 1 봉지로 만들 수 있다.
dp[3] = dp[5] = 1
# 6~N kg까지 정답 구하기
for i in range(6, N + 1):
# 둘다 -1이 아닌 경우에만 min(...) + 1
if dp[i - 3] != -1 and dp[i - 5] != -1:
dp[i] = min(dp[i - 3], dp[i - 5]) + 1
# 둘 중에 하나가 -1인 경우: -1이 아닌 값에 1을 더한다.
elif dp[i - 3] == -1 and dp[i - 5] != -1:
dp[i] = dp[i - 5] + 1
elif dp[i - 3] != -1 and dp[i - 5] == -1:
dp[i] = dp[i - 3] + 1
# 둘다 -1인 경우: 3,5kg로 만들 수 없는 값
else:
dp[i] = -1
# N kg에 대한 정답 출력
print(dp[N])
if __name__ == "__main__":
main()
if...else문을 쓰지 않고 조금 더 엘레강트하게 짤 수 있는 방법이 있다면 알려주세요.